Boom LeetCode入门（三）堆排序&桶排序

发表于 更新于 分类于 阅读次数：

前言

本节详解堆排序和桶排序，堆排序中最关键的就是熟悉堆结构的构建和使用

堆结构&堆排序

算法思路

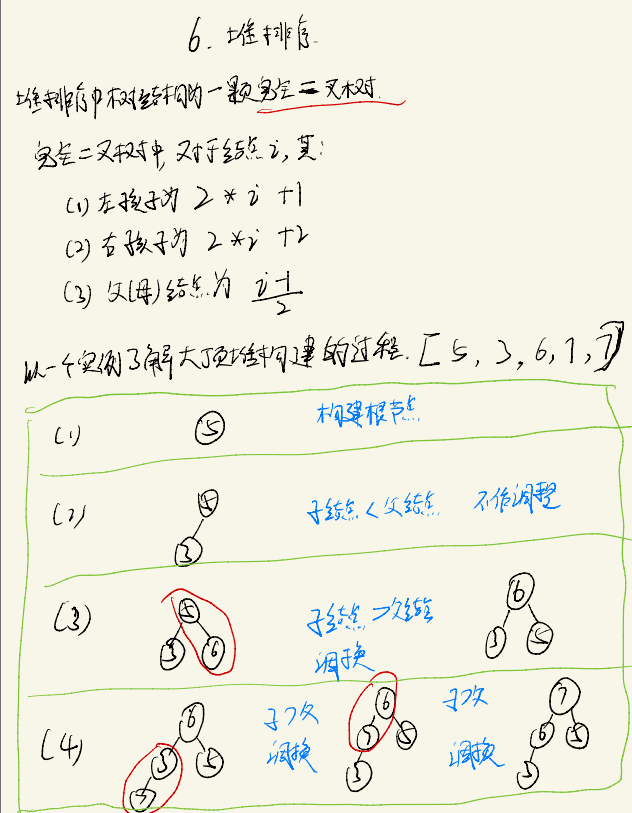
堆结构在逻辑上是一颗完全二叉树， 对于一颗完全二叉树。每一颗子树其根节点为最大值，则该完全二叉树为大根堆。相反，每一颗子树其根节点为最小值，则为小根堆

以大根堆下的堆排序为例，排序算法思路如下：

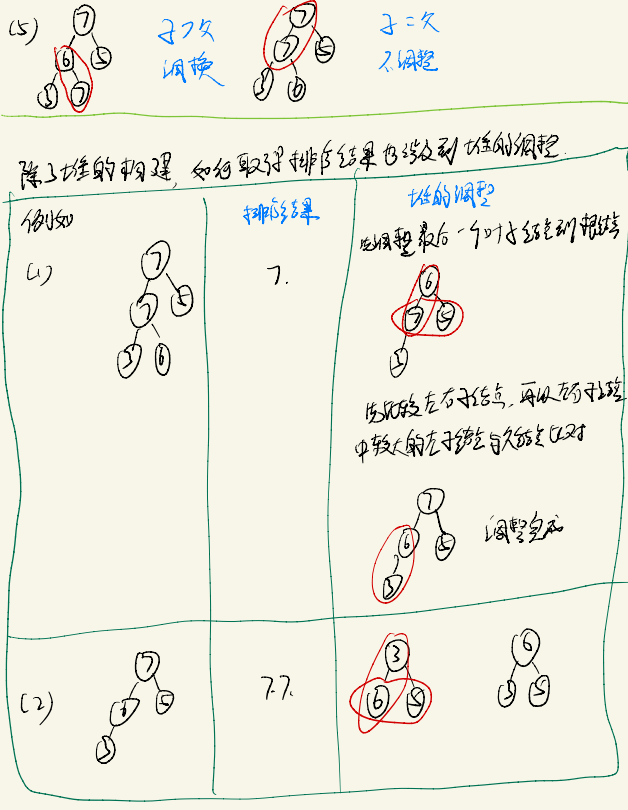
代码实现

大顶堆下的堆排序代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
package p3.heapsort;

import java.util.Scanner;

//堆排序
public class Code01_HeapSort {
    //处理输入输出
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        System.out.println("请输入排序数字个数==========>");
        int n = sc.nextInt();
        int[] nums = new int[n];
        System.out.println("请输入数据============>");
        for (int i = 0; i < n; i++) {
            nums[i] = sc.nextInt();
        }
        heapSort(nums);
        for (int num : nums) {
            System.out.print(num + " ");
        }
    }

    private static void heapSort(int[] nums) {
        //特殊情况
        if(nums == null || nums.length < 2){
            return;
        }

        //构建初始大顶堆
        for (int i = 0; i < nums.length; i++) {
            heapInsert(nums, i);
        }
//        System.out.println("debug======>排序完成");

        //heapSize用来记录堆的右边界，每取完一个最大值，右边界左移一位
        int heapSize = nums.length - 1;
        swap(nums, 0, heapSize--);
        while(heapSize > 0){
            //heapify为取完最大值后，对大顶堆的调整
            heapify(nums, 0, heapSize);
            swap(nums, 0, heapSize--);
        }
    }


    private static void heapInsert(int[] nums, int index) {
        //值不断与父节点比较，直到父节点大于其值，或者到达根节点时，调整结束
        while(nums[index] > nums[(index - 1) / 2]){
            swap(nums, index, (index - 1) / 2);
            index = (index - 1) / 2;
        }
    }

    private static void heapify(int[] nums, int index, int heapSize) {
        int left = index * 2 + 1;
        while(left < heapSize){
            //右子节点存在时，先比较左右子节点，找到最大值
            int largeIdx = (left + 1 < heapSize && nums[left + 1] >nums[left]) ?
                    left + 1 : left;

            //子节点数值小于父节点时，大顶堆调整完毕
            //这里要留意大顶堆结构特性，当父节点数值大于子节点时，当前父节点子树结构未被打乱
            //所以必定大于所有子树节点数值
            if(nums[largeIdx] <= nums[index]){
                break;
            }
            swap(nums, index, largeIdx);
            index = largeIdx;
            left = index * 2 + 1;
        }
    }

    //交换数组数值
    private static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    
}

堆排序下每次调整，在一个树的高度上只有一次，而堆结构又是一颗完全二叉树。

因此堆排序的时间复杂度为

而对于空间复杂度，堆排序下只有在堆结构进行调整时需要额外为几个变量开辟空间，其空间复杂度低

堆结构的重要性体现在它的多个应用场景下，优先级队列就是基于堆结构实现的，其底层结构为小根堆，JAVA中有PriorityQueue具体实现，能够直接调用

JAVA比较器的使用

JAVA中通过Arrays.sort()对一个数组进行排序，返回的结果默认按照升序排列，如何直接得到降序排列结果呢

对于比较器中传入的两个参数a,b(注意传参顺序，a为第一个参数，b为第二参数)，根据返回结果：

  • 为负数时，a排前面
  • 为正数时，b排前面
  • 为0时，都可

那么应用比较器生成大根堆的排序时，就可以将其返回结果看作是：

  • 为负数时，a排上面
  • 为正数时，b排下面
  • 为0时，都可

这样就可以通过传入一个比较器，将PriorityQueue调整为大根堆结构

桶排序

前面提到的所有排序算法只与两个数大小的比较有关，将这些算法统称为基于比较的排序算法，而桶排序就是一种不基于比较的排序算法，需要留意的是：

不基于比较的排序算法，如何实现需要根据数据状况定制

计数排序

对于一个数组，例如[0, 1, 2, 4, 5, 7, 7, 1, 2, 7]

从左往右遍历数组，并记录下每一个数出现的次数

0→1次

1→2次

2→2次

4→1次

5→1次

7→3次

再根据记录的次数得出排序后的数组为[0, 1, 1, 2, 2, 4, 5, 7, 7, 7]

基数排序

算法思路

基数排序为桶排序中最为重要的一种排序算法

其算法思路如下：

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
package p3.heapsort;

import java.util.Arrays;
import java.util.Scanner;

//基数排序
public class Code02_RadixSort {
    public static void main(String[] args) {
//        System.out.println("debug=====>" + getMaxDigit(new int[]{1000}));
        Scanner sc = new Scanner(System.in);
        System.out.println("请输入排序数字个数==========>");
        int n = sc.nextInt();
        int[] nums = new int[n];
        System.out.println("请输入数据============>");
        for (int i = 0; i < n; i++) {
            nums[i] = sc.nextInt();
        }
        radixSort(nums);
        for (int num : nums) {
            System.out.print(num + " ");
        }
    }

    private static void radixSort(int[] nums) {
        if(nums == null || nums.length < 2){
            return;
        }

        final int init = 10;
        int[] help = new int[nums.length];
        //count数组用来记录，每个位置上同一数字的出现数字
        //下标1-9对应出现的数字，下标对应数字为出现次数

        //计算nums数组中最大数的位数
        int maxDigit = getMaxDigit(nums);
        for (int i = 0; i < maxDigit; i++) {
            int[] count = new int[10];
            for (int j = 0; j < nums.length; j++) {
                int num = ((nums[j] / (int)Math.pow(init, i)) % 10);
                count[num] ++;
            }
            for (int j = 1; j < count.length; j++) {
                count[j] = count[j] + count[j-1];
            }
            for(int j = nums.length - 1; j>=0; j--){
                int num = ((nums[j] / (int)Math.pow(init, i)) % 10);
                int numCount = count[num];
                help[numCount - 1] = nums[j];
                count[num]--;
            }
            for (int j = 0; j < help.length; j++) {
                nums[i] = help[i];
            }
        }
    }

    private static int getMaxDigit(int[] nums) {
        int max = nums[0];
        for (int i = 1; i < nums.length; i++) {
            max = Math.max(max, nums[i]);
        }
        int digit = 0;
        while(max != 0){
            digit++;
            max = max / 10;
        }
        return digit;
    }
    
}

radixSort使用了两个数组来辅助排序，分别是count[]用来记录对应下标的数字，在当前位数的排序中出现的次数，不过做了一些调整，记录不是=该数的次数，而是<=该数的次数，为什么要这样保存呢，看一个实例

稳定性

对于排序算法，排序完成后相同值的对应位置没有发生变化，则认为该排序算法是稳定的。例如([1, 2, 3, 1]排序完成后[1, 1, 2, 3],第一个以仍对应的原数组中第一个1，则该排序过程是稳定的)。

稳定的排序算法：冒泡排序、插入排序、归并排序、基数排序

不稳定的排序算法：选择排序、快速排序、堆排序

总结

各排序算法一览表如下：

排序算法 时间复杂度 空间复杂度 稳定性
选择 ×
冒泡 √
插入 √
归并 √
快排3.0 ×
堆 ×

排序算法的回顾到这一part结束，熟悉每个排序算法要解决的问题和算法思路尤为重要。后续将逐步回顾常用数据结构的使用。