Boom LeetCode入门（八）暴力递归

发表于 分类于 阅读次数：

前言

暴力递归，用于求解能够将每一个问题划分为多个子问题，且子问题与主体问题类型一致，在运算的过程中不记录子问题的结果，同时为了避免程序的死循环，暴力递归还应当具备明确的终止递归条件。暴力递归是动态规划的基础

汉诺塔问题

问题：打印n层汉诺塔，从左边移动到最右边的全部过程

解题思路如↓

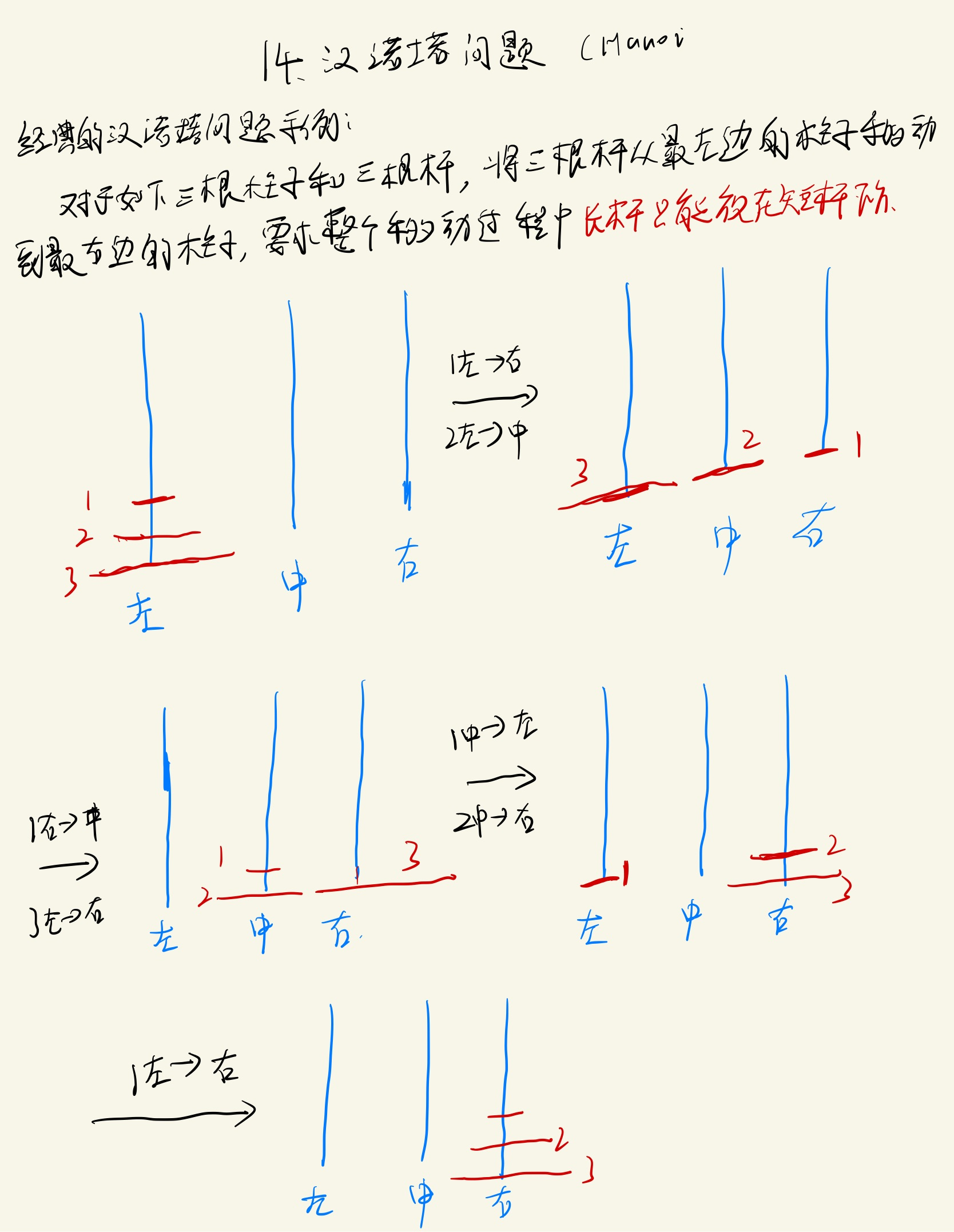
实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
package p9.recursion;

/**
 * @PackageName:p9.recursion
 * @ClassName:Code01_Hanoi
 * @Description:暴力递归求解汉诺塔问题
 * @author:sliu
 * @data 2022/5/24 15:42
 */
public class Code01_Hanoi {
    public static void main(String[] args) {
        //对于有三根柱，三根棍的汉诺塔问题，打印移动顺序
        //i > 0
        hanoi(3, "左", "中", "右");
    }

    private static void hanoi(int i, String start, String other, String end) {
        if(i == 1){
            System.out.println("Move 1 from" + start + "to" + end);
        } else{
            //1~i-1从from放到other
            hanoi(i - 1, start, end, other);
            //i放到最终位置end
            System.out.println("Move " + i + " from " + start + "to" + end);
            //1~i-1从other放到to，继续递归
            hanoi(i - 1, other, start, end);
        }

    }
}

打印子序列

问题：打印一个字符串的全部子序列，包括空字符串

该问题下通过递归，对于字符串中的每一个字符，按照“添加该字符到最终子序列”和“不添加该字符到最终子序列”，两条路径进行递归，对每一个字符按照该方案进行递归求解，得到最终全部子序列，大体过程如下：

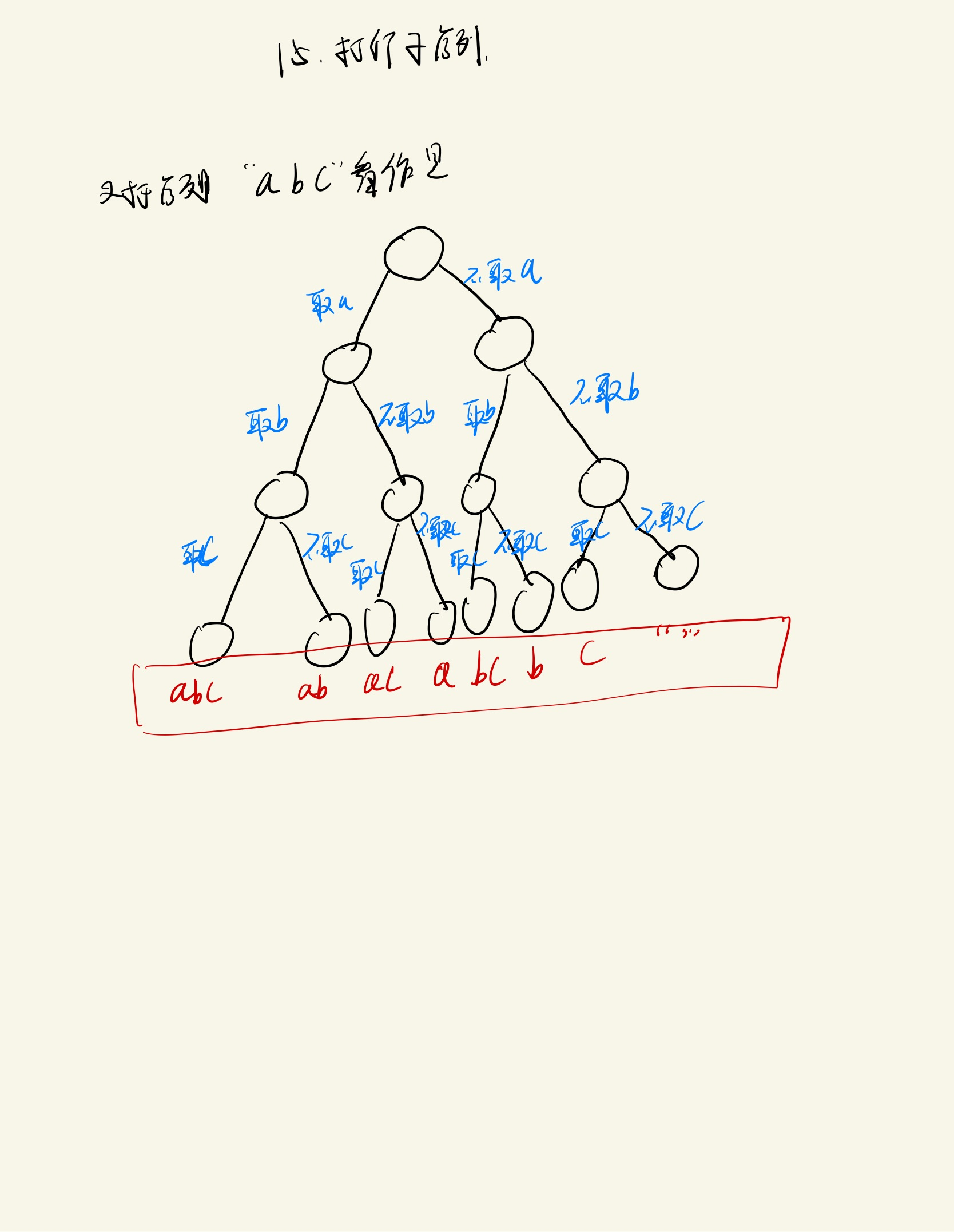
实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
package p9.recursion;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;

/**
 * @PackageName:p9.recursion
 * @ClassName:Code02_PrintAllSubsequence
 * @Description:利用递归打印字符串的全部子序列
 * @author:sliu
 * @data 2022/5/24 16:43
 */
public class Code02_PrintAllSubsequence {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String str = sc.next();
        char[] arr = str.toCharArray();
        printAllSubsequence(arr, 0, new ArrayList<Character>());
    }

    private static void printAllSubsequence(char[] arr, int i, ArrayList<Character> list) {
        if(i == arr.length ){
            printList(list);
            return;
        }
        //添加当前字符进子序列，并继续递归
        ArrayList<Character> keepRes = copyList(list);
        keepRes.add(arr[i]);
        printAllSubsequence(arr, i + 1, keepRes);
        //不添加当前字符进子序列，并继续递归
        ArrayList<Character> notKeepRes = copyList(list);
        printAllSubsequence(arr, i + 1, notKeepRes);
    }

    private static ArrayList<Character> copyList(ArrayList<Character> list) {
        return new ArrayList<>(list);
    }

    private static void printList(ArrayList<Character> list) {
        for (Character c : list) {
            System.out.print(c);
        }
        System.out.println();
    }
}

test：

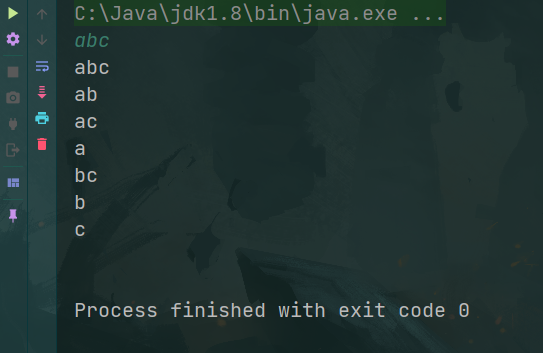
字符串的全排列

问题：打印一个字符串的全部排列

全排列

全排列问题仍然可以利用递归求解，对于长度为n的字符串String中的每一个字符i，0 ~ i为已经确定的字符串，而后续逐步选取i+1~n上的每一个字符拼接到i+1的位置上完成排列，需要注意的是递归返回时，应当交换回字符位置，以复原初始字符串

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        if(nums == null){
            return res;
        }
        process(nums, 0, res);
        return res;
    }

    public void process(int[] nums, int i, List<List<Integer>> res){
        if(i == nums.length){
            List<Integer> temp = new ArrayList<Integer>();
            for (int num : nums) {
                temp.add(num);
            }
            res.add(temp);
            return;
        }
        for(int j = i; j < nums.length; j++){
            swap(nums, i, j);
            process(nums, i + 1, res);
            swap(nums, i, j);
        }
        return;
    }

    public void swap(int[] nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

编码过程中遇到了多维数组的初始化问题，如何解决戳多维List数组的初始化

直接抄作业，能够使用的两种初始化方式：

1
2
3
List<List<Integer>> list = new ArrayList<List<Integer>>();

List<List<Integer>> list = new ArrayList<>(); //没有Integer

List是接口，ArrayList实现了这个接口，所以不能直接使用的初始化方式：

1
2
3
List<List<Integer>> list = new List<List<Integer>>();

List<List<Integer>> list = new ArrayList<ArrayList<Integer>>();

纸牌游戏

定义两个函数，先手函数F(arr, L, R)用于返回数组arr中L-R范围内先手时能够获得的最大数，后手函数S(arr, L, R)用于返回后手时所能获得的数

其中F函数下：

  • 当L==R时，只有一张牌，且为先手，直接返回这张牌的数值即可
  • 否则，返回和中的最大值

而S函数下：

  • 当L==R时，只有一张牌，且为后手，无法取得这张牌，返回0
  • 否则，返回和中的最小值（因为对方也是懂策略的人，总能取得最大值）

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
package p9.recursion;

/**
 * @PackageName:p9.recursion
 * @ClassName:Code03_PokeGame
 * @Description:利用递归求解扑克游戏
 * @author:sliu
 * @data 2022/5/24 20:55
 */
public class Code03_PokeGame {
    public int f(int[] arr, int l, int r){
        if(l == r){
            return arr[l];
        }
        return Math.max(arr[l] + s(arr, l + 1, r), arr[r] + s(arr, l, r - 1));
    }
    
    public int s(int[] arr, int l, int r){
        if(l == r){
            return 0;
        }
        return Math.min(arr[l] + f(arr, l + 1, r), arr[r] + f(arr, l, r - 1));
    }
}

递归实现栈的逆序

问题：给出一个栈的逆序，要求不能申请额外的数据结构，只能使用递归函数

解题思路：先分析如何将一个栈中，如何返回栈底元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public static void main(String[] args) {
        Stack<Integer> stack = new Stack();
        stack.push(3);
        stack.push(2);
        stack.push(1);
        int last = swapFootTop(stack);
        while(!stack.isEmpty()){
            System.out.println(stack.pop());
        }
        System.out.println(last);
    }

    public static int swapFootTop(Stack<Integer> stack){
        int result = stack.pop();
        if(stack.isEmpty()) {
            return result;
        }else{
            int last = swapFootTop(stack);
            stack.push(result);
            return last;
        }
    }

这样，利用栈返回栈底元素时元素入栈，最终完成逆序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
package p9.recursion;

import java.util.Stack;

/**
 * @PackageName:p9.recursion
 * @ClassName:Code04_ReverseStack
 * @Description:栈的逆序
 * @author:sliu
 * @data 2022/5/27 14:51
 */
public class Code04_ReverseStack {
    public static void main(String[] args) {
        Stack<Integer> stack = new Stack();
        stack.push(3);
        stack.push(2);
        stack.push(1);
        reverse(stack);
//        int last = swapFootTop(stack);
        while(!stack.isEmpty()){
            System.out.println(stack.pop());
        }
//        System.out.println(last);
    }

    private static void reverse(Stack<Integer> stack) {
        if(stack.isEmpty()){
            return;
        }
        int last = swapFootTop(stack);
        reverse(stack);
        stack.push(last);
    }

    public static int swapFootTop(Stack<Integer> stack){
        int result = stack.pop();
        if(stack.isEmpty()) {
            return result;
        }else{
            int last = swapFootTop(stack);
            stack.push(result);
            return last;
        }
    }
}

数字转字符

问题：规定1和A对应，2和B对应，3和C对应......

那么一个数字字符串，例如“111”，能够转化成“AAA”、“KA”、“AK”

给定一个只有数字的字符串，返回有多少种转化结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
package p9.recursion;

/**
 * @PackageName:p9.recursion
 * @ClassName:Code05_NumConvertToWord
 * @Description:数字转字符，组合方式
 * @author:sliu
 * @data 2022/5/27 16:41
 */
public class Code05_NumConvertToWord {
    public static void main(String[] args) {
        //AAAAA AKAA AKK AAK KKA KAAA AAKA AAAK
        System.out.println(convert("11111", 0));
    }

    private static int convert(String s, int i) {
        if(i == s.length()){
            return 1;
        }
        if(s.charAt(i) == '0'){
            return 0;
        }
        if(s.charAt(i) == '1'){
            int res = convert(s, i + 1);//i自己作为单独的部分，有多少种转换方法
            if(i + 1 < s.length()){
                res += convert(s, i + 2);//i和i+1作为一个部分，有多少种转换方法
            }
            return res;
        }
        if(s.charAt(i) == '2'){
            int res = convert(s, i + 1);//i自己作为单独的部分，有多少种转换方法
            //只有20 - 26算入字符
            if(i + 1 < s.length() && s.charAt(i + 1) >= '0' && s.charAt(i + 1) <= '6'){
                res += convert(s, i + 2);//i和i+1作为一个部分，有多少种转换方法
            }
            return res;
        }
        //s[i]为‘3’到‘9’时，只能自己作为单独的部分
        return convert(s, i + 1);
    }
}

背包最大价值问题

问题描述：给定两个长度都为N的数组weights和values，分别代表对应数组下标物品的重量和价值。给定一个正数bag，表示一个载重bag的袋子，袋子能装下的物品总量不能超过这个重量。返回你能装下最多的价值是多少？

思路：记录对于每一个物品，放入背包和不放入背包的总价值，比较并选取最大化价值的放入方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
package p9.recursion;

/**
 * @PackageName:p9.recursion
 * @ClassName:Code06_NPackage
 * @Description:递归求解背包最大价值问题
 * @author:sliu
 * @data 2022/5/27 17:03
 */
public class Code06_NPackage {
    public int getMaxWeight(int[] weights, int[] values, int i, int curWeight, int bag){
        //重量超过bag时，不能放入该物品
        if(curWeight > bag){
            return 0;
        }
        //物品选取完毕，返回0
        if(i > values.length){
            return 0;
        }
        //不放入当前物品和放入中，选择能够最大化最终value的方案
        return Math.max(
                //不放入当前物品
                getMaxWeight(weights, values, i + 1, curWeight, bag),
                //放入当前物品
                values[i] + getMaxWeight(weights, values, i +1, curWeight + weights[i], bag)
        );
    }
}

N皇后问题

再次回到N皇后问题

暴力求解

每一行逐列探索，最后累加所有可能的结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
package p7.preTreeAndGreedy;

/**
 * @PackageName:p7.preTreeAndGreedy
 * @ClassName:Code05_NQueen
 * @Description:N皇后问题
 * @author:sliu
 * @data 2022/5/21 22:19
 */
public class Code05_NQueen {
    public int getMaxNQueen(int n){
        if(n == 0){
            return 0;
        }
        //recode[i]表示第i行的Queen放在第几列
        int[] record = new int[n];
        return simProcess(0, record, n);
    }

    //暴力遍历求解N皇后问题
    public int simProcess(int i, int[] record, int n){
        if(i == n){
            return 1;
        }
        int res = 0;
        for (int j = 0; j < n; j++) {
            if(isValid(record, i, j)){
                record[i] = j;
                res += simProcess(i + 1, record, n);
            }
        }
        return res;
    }

    //验证当前位置是否符合放置规范
    private boolean isValid(int[] record, int i, int j) {
        for (int k = 0; k < i; k++) {
            //如果在同一列或同一条斜线上，不合法
            //同一斜线上的验证，通过判断斜率是否为1判定
            if(k == j || Math.abs(record[k] - j) == Math.abs(i - k)){
                return false;
            }
        }
        return true;
    }
}

总结

本part学习了递归函数的使用，递归核心特征在于其能够保留历史处理数据，对于需要借助历史数据求解问题的场景中，借助递归能够很大程度上降低程序时间复杂度，是对暴力求解方法的优化