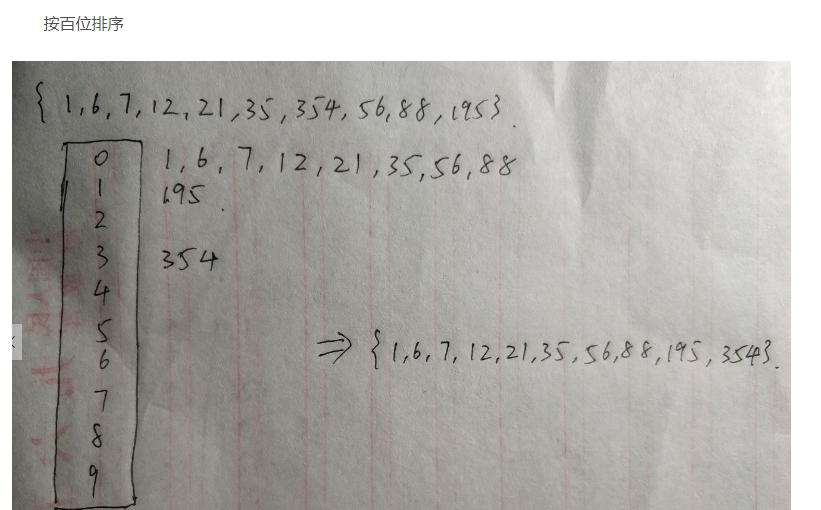摘要
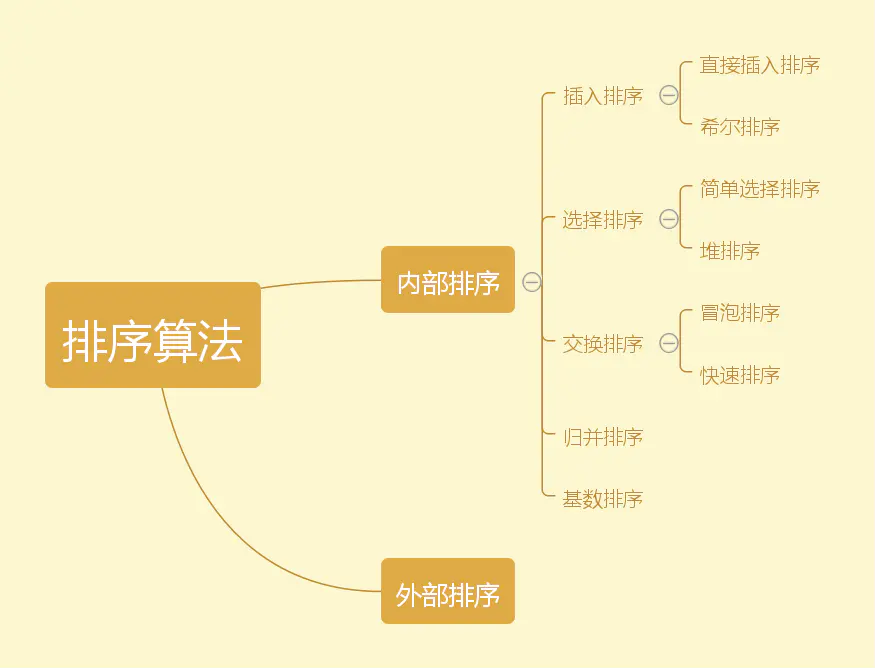
分类
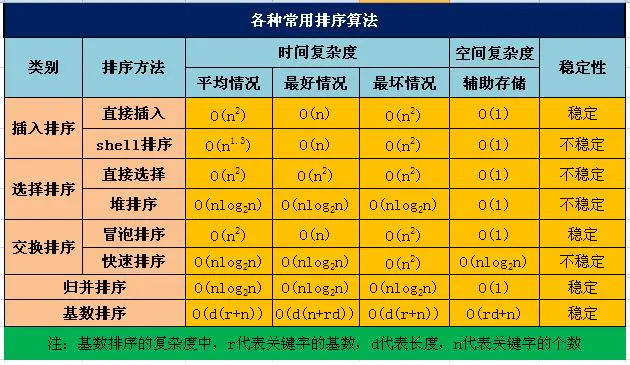
- 性能分析
实现
插入排序
直接插入排序
直接插入排序的核心思想就是:将数组中的所有元素依次跟前面已经排好的元素相比较,如果选择的元素比已排序的元素小,则交换,直到全部元素都比较过。
因此,从上面的描述中我们可以发现,直接插入排序可以用两个循环完成:
- 第一层循环:遍历待比较的所有数组元素
- 第二层循环:将本轮选择的元素(selected)与已经排好序的元素(ordered)相比较。
如果:selected > ordered,那么将二者交换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public class insert_sort {
public static void main(String[] args) {
int[] arr = {2,5,9,3,4,10,8};
for(int i = 1; i<arr.length; i++){
for(int j = i - 1; j >= 0; j--){
if(arr[j] > arr[j+1]){
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
for (int i : arr) {
System.out.print(i+" ");
}
}
}
|
希尔(shell)排序
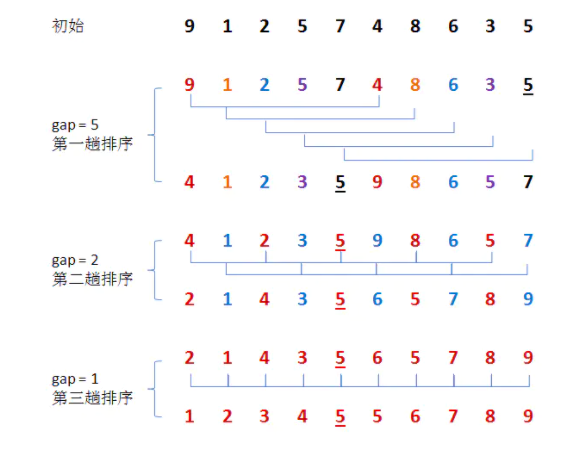
算法思想:
将待排序数组按照步长gap进行分组,然后将每组的元素利用直接插入排序的方法进行排序;每次将gap折半减小,循环上述操作;当gap=1时,利用直接插入,完成排序。
同样的:从上面的描述中我们可以发现:希尔排序的总体实现应该由三个循环完成:
- 第一层循环:将gap依次折半,对序列进行分组,直到gap=1
- 第二、三层循环:也即直接插入排序所需要的两次循环。具体描述见上。
选择排序
直接选择排序
基本思想:比较+交换。
- 从待排序序列中,找到关键字最小的元素;
- 如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换;
- 从余下的 N - 1
个元素中,找出关键字最小的元素,重复(1)、(2)步,直到排序结束。
因此我们可以发现,简单选择排序也是通过两层循环实现。
第一层循环:依次遍历序列当中的每一个元素
第二层循环:将遍历得到的当前元素依次与余下的元素进行比较,符合最小元素的条件,则交换。
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public static void selectSort(int[] numbers)
{
int size = numbers.length;
int temp = 0 ;
for(int i = 0 ; i < size ; i++)
{
int k = i;
for(int j = size -1 ; j > i ; j--)
{
if(numbers[j] < numbers[k])
{
k = j;
}
}
temp = numbers[i];
numbers[i] = numbers[k];
numbers[k] = temp;
}
}
|
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序。
首先我们来了解下什么是堆。
堆分为两种:大顶堆和小顶堆,两者的差别主要在于排序方式。
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
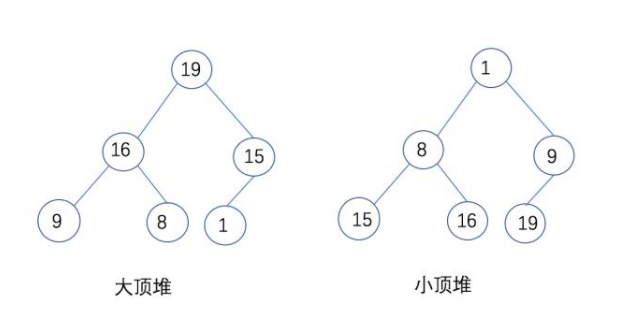
大顶堆的存储结构为:{19,16,15,9,8,1}
小顶堆的存储结构为:{1,8,9,15,16,19}
我举的是两个有序的例子,当然,大顶堆和小顶堆的存储结构未必是有序的,只要父节点大于他的左右孩子节点就是大顶堆了,父节点小于他的孩子左右孩子节点就是小顶堆。
堆排序的基本思想和步骤
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
下面我们举例来说明堆排序的步骤。
给定序列{15,8,1,19,16,9}
首先根据序列构造一个完全二叉树。

根据大顶堆的原理,我们构造一个大顶堆,此时我们从最后一个非叶子节点开始,如下图。
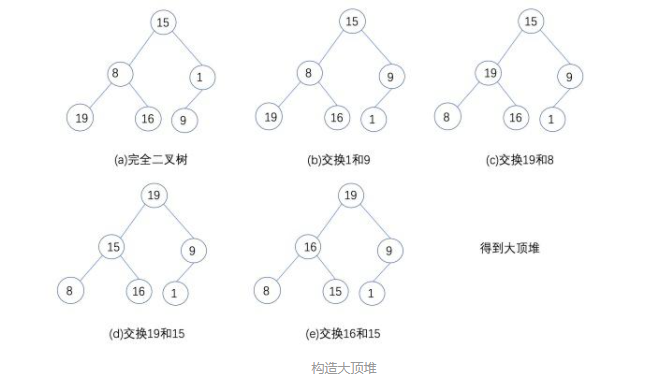
大顶堆的存储结构为{19,16,9,8,15,1}
然后我们将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换,步骤如下。
第一步:将堆顶元素19和堆底元素1交换,然后再重建,得到新的大顶堆,存储结构为:{16,15,9,8,1,19}。
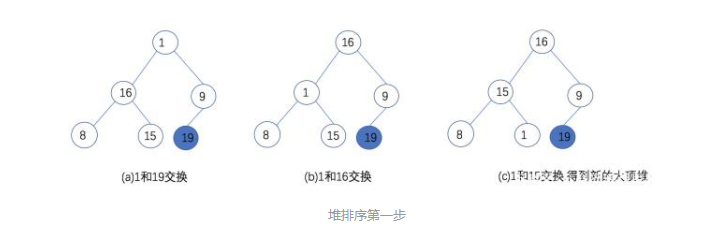
第二步:将堆顶元素16和新的无序堆的堆底元素1交换,然后再重建,得到新的大顶堆,存储结构为:{15,8,9,1,16,19}
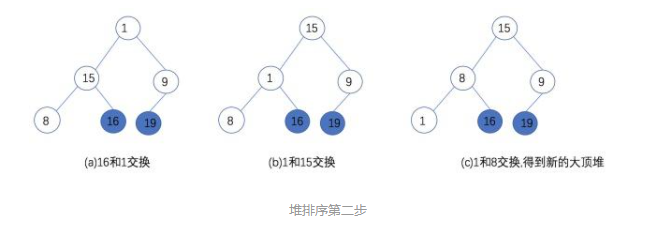
第三步:将堆顶元素15和新的无序堆的堆底元素1交换,然后再重建,得到新的大顶堆,存储结构为:{9,8,1,15,16,19}
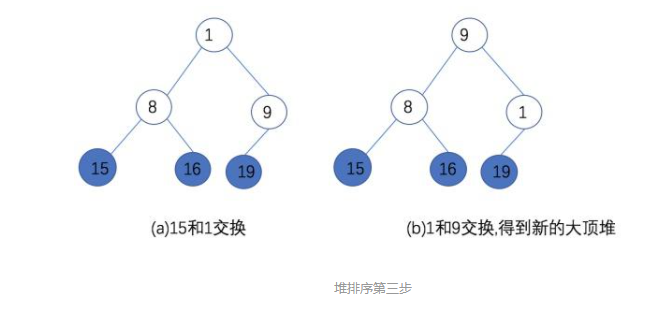
第四步:将堆顶元素9和新的无序堆的堆底元素1交换,然后再重建,得到新的大顶堆,存储结构为:{8,1,9,15,16,19}
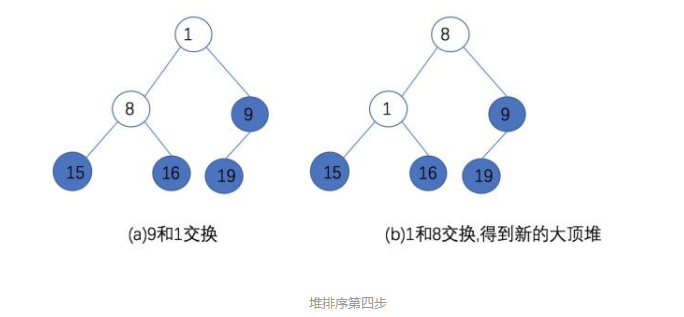
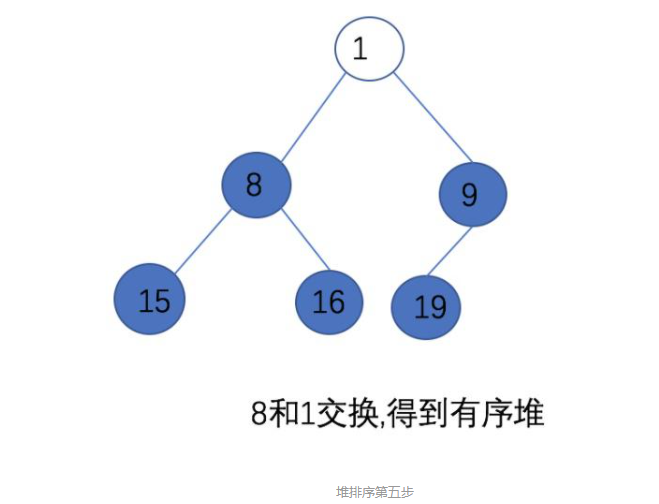
第五步,将堆顶元素8和新的无序堆的堆底元素1交换,交换后整个堆为有序,存储结构为:{1,8,9,15,16,19}。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| package demo01.paixu;
public class HeapSort {
public static void main(String[] args) {
int[] arr = {19,16,15,9,8,1};
sort(arr);
for (int i : arr) {
System.out.println(i);
}
}
public static void sort(int[] arr){
for(int i = arr.length / 2 - 1; i >= 0; i--){
adjustHead(arr,i,arr.length);
}
for (int j = arr.length - 1; j > 0; j--){
swap(arr, 0, j);
adjustHead(arr, 0, j);
}
}
public static void adjustHead(int arr[], int i, int len){
int tmp = arr[i];
for(int k = i * 2 + 1; k < len; k = k * 2 + 1){
if(k + 1 < len && arr[k + 1] > arr[k]){
k++;
}
if(arr[k] > tmp){
arr[i] = arr[k];
i = k;
}else{
break;
}
}
arr[i] = tmp;
}
public static void swap(int[] arr, int a, int b){
int tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
}
|
交换排序
冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
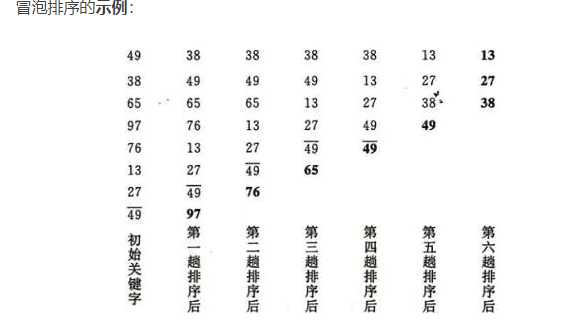
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public static void bubbleSort(int[] numbers)
{
int temp = 0;
int size = numbers.length;
for(int i = 0 ; i < size-1; i ++)
{
for(int j = 0 ;j < size-1-i ; j++)
{
if(numbers[j] > numbers[j+1])
{
temp = numbers[j];
numbers[j] = numbers[j+1];
numbers[j+1] = temp;
}
}
}
}
|
快速排序
快速排序的基本思想:
通过一趟排序将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分关键字小,则分别对这两部分继续进行排序,直到整个序列有序。

把整个序列看做一个数组,把第零个位置看做中轴,和最后一个比,如果比它小交换,比它大不做任何处理;交换了以后再和小的那端比,比它小不交换,比他大交换。这样循环往复,一趟排序完成,左边就是比中轴小的,右边就是比中轴大的,然后再用分治法,分别对这两个独立的数组进行排序。
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
public static int getMiddle(int[] numbers, int low,int high)
{
int temp = numbers[low];
while(low < high)
{
while(low < high && numbers[high] >= temp)
{
high--;
}
numbers[low] = numbers[high];
while(low < high && numbers[low] < temp)
{
low++;
}
numbers[high] = numbers[low] ;
}
numbers[low] = temp ;
return low ;
}
|
归并排序
基本思想:
归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
归并排序示例:
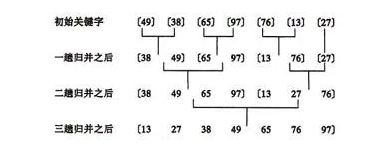
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| package demo01.paixu;
public class gb {
public static void main(String[] args) {
int[] arr = {9,98,6,8,2,5,4};
int[] res = sort(arr,0, arr.length-1);
for (int i : res) {
System.out.println(i);
}
}
public static int[] sort(int nums[], int low, int high){
int mid = (low + high) / 2;
if(low < high){
sort(nums, low, mid);
sort(nums, mid + 1, high);
merge(nums, low, mid, high);
}
return nums;
}
public static void merge(int[] nums, int low, int mid, int high){
int[] tmp = new int[high - low + 1];
int i = low;
int j = mid + 1;
int k = 0;
while(i <= mid && j <= high) {
if (nums[i] < nums[j]) {
tmp[k++] = nums[i++];
} else {
tmp[k++] = nums[j++];
}
}
while (i <= mid){
tmp[k++] = nums[i++];
}
while(j <= high){
tmp[k++] = nums[j++];
}
for(int k2 = 0; k2 < tmp.length; k2++){
nums[k2 + low] = tmp[k2];
}
}
}
|
基数排序
假定现在有这样一个整型数组{21,56,88,195,354,1,35,12,6,7},我们可以看到,最大的数,354,是三位数,也就是说,这个排序最大涉及的数就是一个三位数,那么我们该怎么对这个数组运用基数排序呢?
首先,看这些数的个位,把他们按照个位从小到大排序(注意是按照个位),具体怎么排咱们一会儿看代码,先说原理,
也就是说,原来的数组按照个位排序就变成了{21,1,12,354,195,35,56,6,7,88}

从前往后,21,放到1号桶中(我们姑且先把他叫做桶),56放到6号桶中,88放到8号桶……放完之后,再把他们按顺序拿出来,就变成了{21,1,12,354,195,35,56,6,7,88},很好理解,对吧,之后再按照这样的方法,把十位,百位,都排一遍,当你排完百位的时候,你就发现,数组变得有序了

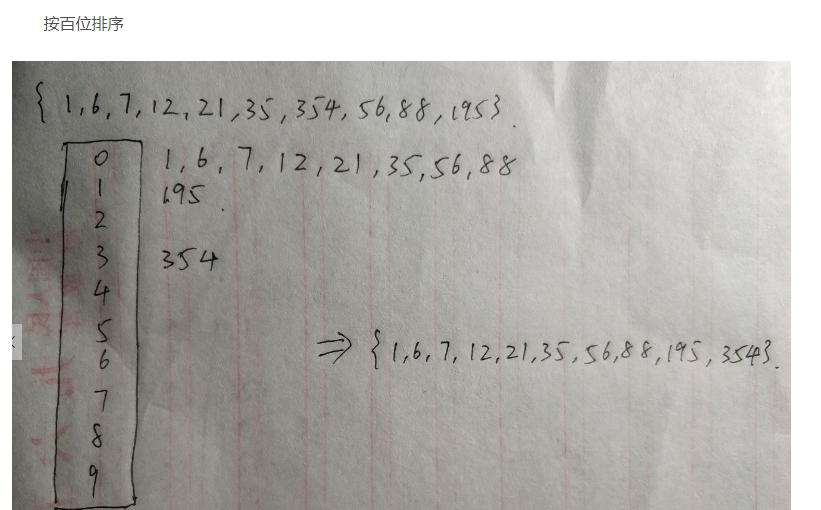
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
|
class Demo
{
public static void main(String[] args)
{
int[] arr = {21,56,88,195,354,1,35,12,6,7};
lsd_RadixSort(arr,3);
for(int i=0;i<arr.length;i++)
{
System.out.print(arr[i]+" ");
}
}
public static void lsd_RadixSort(int[] arr,int max)
{
int[] count = new int[arr.length];
int[] bucket = new int[arr.length];
for(int k=1;k<=max;k++)
{
for(int i=0;i<arr.length;i++)
{
count[i] = 0;
}
for(int i=0;i<arr.length;i++)
{
count[getFigure(arr[i],k)]++;
}
for(int i=1;i<arr.length;i++)
{
count[i] = count[i] + count[i-1];
}
for(int i=arr.length-1;i>=0;i--)
{
int j = getFigure(arr[i],k);
bucket[count[j]-1] = arr[i];
count[j]--;
}
for(int i=0,j=0;i<arr.length;i++,j++)
{
arr[i] = bucket[j];
}
}
}
public static int getFigure(int i,int k)
{
int[] a = {1,10,100};
return (i/a[k-1])%10;
}
|