Boom LeetCode入门（六）图

发表于 更新于 分类于 阅读次数：

前言

对于图的算法，在图的不同表示结构下（例如邻接表和邻接矩阵）有不同的具体实现方式，但是具体的算法思路是一致的，因而在学习过程中只需要掌握好一种结构下的具体实现，在面对其它结构时，将其结构调整到我们所熟悉的那一种就能够搞定它。

本part中的算法均使用以下图结构实现：

Node节点结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
package p6.graph;

import java.util.ArrayList;

public class Node {
    //节点的值
    public int value;
    //节点入度
    public int in;
    //节点出度
    public int out;
    //与该节点有边相连接的节点集合(该节点指向的节点，即以该点为起点)
    public ArrayList<Node> nexts;
    //该节点的边集合，以该节点为起点的边
    public ArrayList<Edge> edges;

    public Node(int value){
        this.value = value;
        in = 0;
        out = 0;
        nexts = new ArrayList<>();
        edges = new ArrayList<>();
    }
}

Edge边结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
package p6.graph;

public class Edge {
    //边的权重
    public int weight;

    //边的入节点
    public Node from;

    //边的出节点
    public Node to;

    public Edge(int weight, Node from, Node to){
        this.weight = weight;
        this.from = from;
        this.to = to;
    }
}

Graph图结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
package p6.graph;

import java.util.HashMap;
import java.util.HashSet;

public class Graph {
    //点集合<节点标号，节点>
    public HashMap<Integer, Node> nodes;

    //边集合
    public HashSet<Edge> edges;

    public Graph(){
        nodes = new HashMap<>();
        edges = new HashSet<>();
    }

}

图的遍历

对于如下图，其BFS序列为[A, B, C, D, E, F]，其中，同一层次的遍历顺序不分先后(例如，也可以为[A, B, D, C, E, F])

DFS序列为[A, B, E, C, F, D]，与BFS相同，DFS序列也能够存在多个不同序列

图的BFS↓

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
package p6.graph;

import java.util.HashSet;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Set;

/**
 * @PackageName:p6.graph
 * @ClassName:GraphBfs
 * @Description:图的广度优先遍历
 * @author:sliu
 * @data 2022/5/14 14:26
 */
public class GraphBfs {
    public void graphBfs(Node node){
        if(node == null) return;
        Set<Node> set = new HashSet<>();
        Queue<Node> queue = new LinkedList<>();
        set.add(node);
        queue.offer(node);
        while(!queue.isEmpty()){
            node = queue.poll();
            System.out.println(node.value);
            for (Node temp : node.nexts) {
                if(!set.contains(temp)){
                    set.add(temp);
                    queue.offer(temp);
                }
            }
        }
    }
}

以set存储节点并逐一比对，便于区分图中是否有环

图的DFS↓

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
package p6.graph;

import java.util.*;

/**
 * @PackageName:p6.graph
 * @ClassName:Code02_GraphDFS
 * @Description:图的深度优先遍历
 * @author:sliu
 * @data 2022/5/14 14:46
 */
public class Code02_GraphDFS {
    public void graphDfs(Node node){
        if(node == null) return;
        Set<Node> set = new HashSet<>();
        Stack<Node> stack = new Stack<>();
        set.add(node);
        stack.push(node);
        System.out.println(node.value);
        while(!stack.isEmpty()){
            node = stack.pop();
            for (Node temp : node.nexts) {
                if(!set.contains(temp)){
                    stack.push(temp);
                    set.add(temp);
                    System.out.println(temp.value);
                    stack.push(node);
                    break;
                }
            }
        }
    }
}

拓扑排序算法

拓扑排序仅适用于无环图

拓扑排序常用于有依赖项的应用中，例如对于一个工程，工程B完成后，才能开始A工程，那么应当保证工程的正确执行顺序以避免阻塞，拓扑排序算法思路如下：

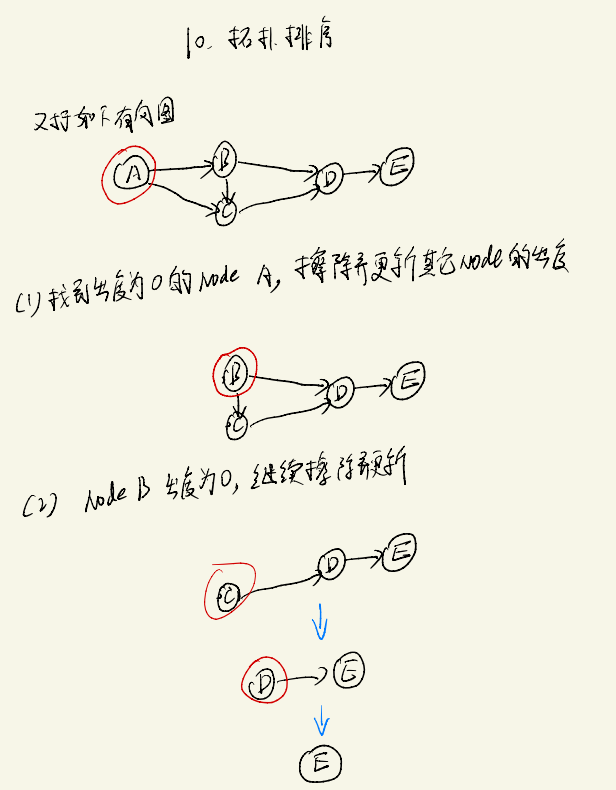
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
package p6.graph;

import java.util.*;

/**
 * @PackageName:p6.graph
 * @ClassName:Code03_TopoSort
 * @Description:图的拓扑排序
 * @author:sliu
 * @data 2022/5/14 15:12
 */
public class Code03_TopoSort {
    public ArrayList<Node> topoSort(Graph graph){
        if(graph == null) return null;
        //以HashMap存储对应节点，当前的出度
        Map<Node, Integer> map = new HashMap<>();
        //用队列存储当前出度为0的节点
        Queue<Node> queue = new LinkedList<>();

        for (Node node : graph.nodes.values()) {
            map.put(node, node.out);
            if(node.out == 0){
                queue.offer(node);
            }
        }

        ArrayList<Node> res = new ArrayList<>();

        while(!queue.isEmpty()){
            //取出出度为0的Node
            Node temp = queue.poll();
            res.add(temp);
            //更新其它Nodes出度
            for (Node next : temp.nexts) {
                map.put(next, map.get(next) - 1);
                if(map.get(next) == 0){
                    queue.offer(next);
                }
            }
        }
        return res;
    }
}

最小生成树

求最小生成树的算法有Kruskal算法和Prim算法，两种算法均用于无向图中，区别在于K算法以边为参考，而P算法以点为参考

Kruskal算法

算法思路如下：

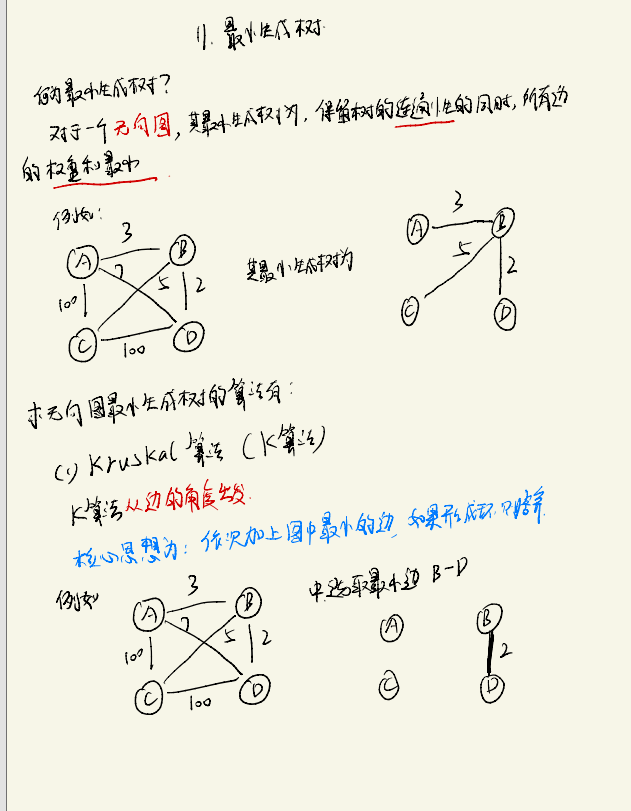
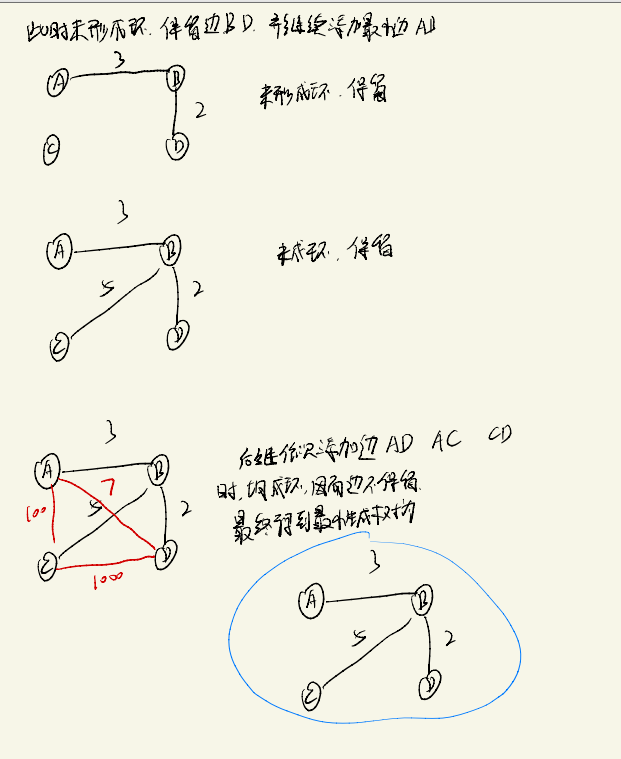
实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
package p6.graph;

import java.util.*;

/**
 * @PackageName:p6.graph
 * @ClassName:Code04_Kruskal
 * @Description:
 * @author:sliu
 * @data 2022/5/14 15:49
 */
public class Code04_Kruskal {
    //初始化set结构用于判断是否形成了环
    public Map<Node, Set<Node>> mySet(Graph graph){
        if(graph == null) return null;
        //HashMap用来存储节点所在集合
        Map<Node, Set<Node>> map = new HashMap<>();
        for (Node node : graph.nodes.values()) {
            Set<Node> set = new HashSet<>();
            set.add(node);
            map.put(node, set);
        }
        return map;
    }

    //判断两个节点是否位于同一集合内，即是否有环
    public boolean isSameSet(Map<Node, Set<Node>> map, Node A, Node B){
        return map.get(A) == map.get(B);
    }

    //合并两个集合
    public void union(Map<Node, Set<Node>> map, Node A, Node B){
        Set<Node> fromSet = map.get(A);
        Set<Node> toSet = map.get(B);
        for (Node node : toSet) {
            if(!fromSet.contains(node)){
                fromSet.add(node);
            }
        }
        map.put(B, fromSet);
    }

    //通过自定义比较器，实现优先队列中的边升序排列
    public class myComparator implements Comparator<Edge>{
        @Override
        public int compare(Edge o1, Edge o2) {
            return o1.weight - o2.weight;
        }
    }

    //Kruskal算法核心
    public Set<Edge> kruskal(Graph graph){
        if(graph == null) return null;
        Map<Node, Set<Node>> map = mySet(graph);
        Set<Edge> res = new HashSet<>();
        PriorityQueue<Edge> queue = new PriorityQueue<>(new myComparator());
        for (Edge edge : graph.edges) {
            queue.add(edge);
        }
        while (!queue.isEmpty()){
            Edge edge = queue.poll();
            
            //边对应的两个节点不在同一集合中时，加入res中并合并两个集合
            if(!isSameSet(map, edge.from, edge.to)){
                res.add(edge);
                union(map, edge.from, edge.to);
            }
        }
        return res;
    }
}

Prim算法

算法思路如下：

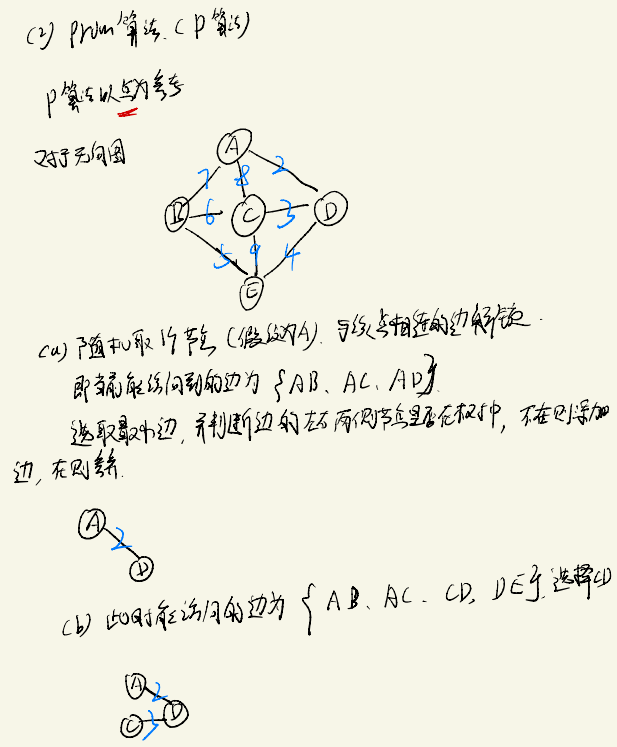
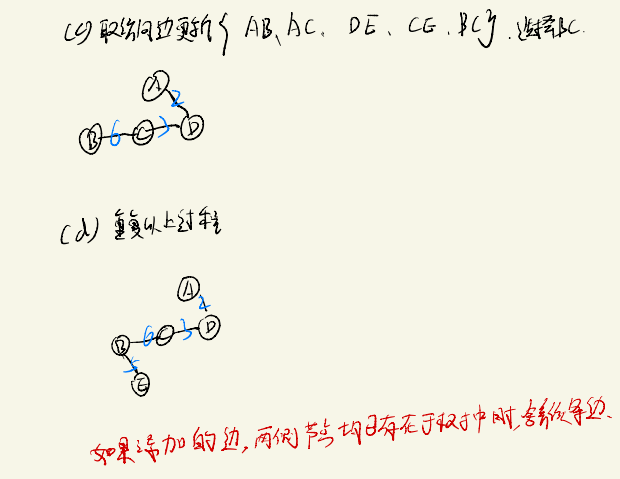
实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
package p6.graph;

import java.util.Comparator;
import java.util.HashSet;
import java.util.PriorityQueue;
import java.util.Set;

/**
 * @PackageName:p6.graph
 * @ClassName:Code05_Prim
 * @Description:Prime算法求最小生成树
 * @author:sliu
 * @data 2022/5/14 16:51
 */
public class Code05_Prim {
    public class myComparator implements Comparator<Edge>{

        @Override
        public int compare(Edge o1, Edge o2) {
            return o1.weight - o2.weight;
        }
    }

    public Set<Edge> prim(Graph graph){
        if(graph == null) return null;

        //set用于存放已放入最小生成树中的节点
        Set<Node> set = new HashSet<>();

        PriorityQueue<Edge> queue = new PriorityQueue<>(new myComparator());
        Set<Edge> res = new HashSet<>();
        for (Node node : graph.nodes.values()) {
            //随机选择一个节点
            if(!set.contains(node)){
                set.add(node);
                //节点所连边全部入队
                for (Edge edge : node.edges) {
                    queue.add(edge);
                }
                while(!queue.isEmpty()){
                    Edge edge = queue.poll();
                    //最小边两侧节点没有加入最小树中时
                    if(!set.contains(edge.to)){
                        res.add(edge);
                        set.add(edge.to);
                        for (Edge temp : edge.to.edges) {
                            queue.offer(temp);
                        }
                    }
                }
            }
        }
        return res;
    }
}

prim函数中的for循环是为了防止出现无连通图，对其中的森林进行处理，逐一生成最小生成树

最短路径

求两个节点之间的最短路径，利用Dijkstra算法和Floyd算法求解

Dijkstra算法

Dijkstra算法适用于没有负数权值边(可以有累加值为负数的边，但不能有累加值为负数的环)的图，给定一个起始节点，求该起始节点到所有节点的最小路径

其算法思想如↓

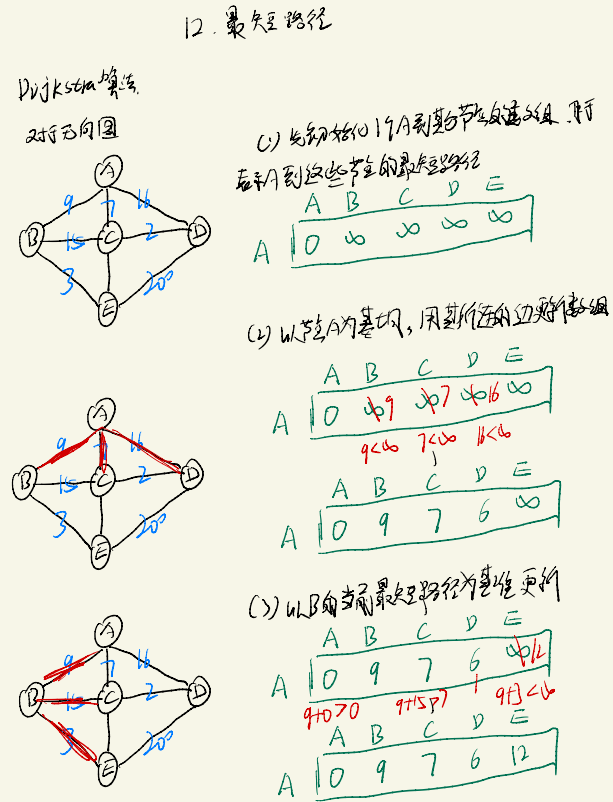
实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
package p6.graph;

import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;

/**
 * @PackageName:p6.graph
 * @ClassName:Code06_Dijkstra
 * @Description:Dijkstra算法求最短路径
 * @author:sliu
 * @data 2022/5/14 18:48
 */
public class Code06_Dijkstra {
    //返回Map中，Value为head到该Value对应节点的最短路径
    public HashMap<Node, Integer> dijkstra(Node head){
        if(head == null) return null;
        HashMap<Node, Integer> map = new HashMap<>();
        //到自己的最短距离为0
        map.put(head, 0);
        //selectedSet记录当前已被作为基准，使用过的节点
        HashSet<Node> selectedSet = new HashSet<>();
        //返回当前节点所对应的最短边所连接的节点（且该节点未作为基准使用过）
        Node minNode = getMinEdgeAndNoSelectedNode(map, selectedSet);

        while(minNode != null){
            //当前基准节点的最短路径
            int distance = map.get(minNode);
            //更新该基准节点所连接到的节点其最短距离
            for (Edge edge : minNode.edges) {
                Node toNode = edge.to;
                if(!map.containsKey(toNode)){
                    map.put(toNode, distance + edge.weight);
                }else{
                    map.put(toNode, Math.min(map.get(toNode), distance + edge.weight));
                }
            }
            selectedSet.add(minNode);
            //继续选择下一个基准节点，直到所有节点都使用过，返回null，结束
            minNode = getMinEdgeAndNoSelectedNode(map, selectedSet);
        }
        return map;
    }

    private Node getMinEdgeAndNoSelectedNode(HashMap<Node, Integer> map, HashSet<Node> selectedSet) {
        Node minNode = null;
        int minDistance = Integer.MAX_VALUE;
        for (Map.Entry<Node, Integer> entry : map.entrySet()) {
            Node temp = entry.getKey();
            if(map.get(temp) < minNode.value && selectedSet.contains(temp)){
                minNode = temp;
                minDistance = map.get(temp);
            }
        }
        return minNode;
    }
}

总结

该part中详细介绍了图结构的使用，以及常见的图相关算法，其中较为关键的是要能够熟练掌握一种自己所熟悉图结构下算法的具体实现，并能够将其它图结构转化为自己所熟悉的结构