前言
Boom
LeetCode(一)中介绍了常用排序算法选择排序、冒泡排序和插入排序,这些排序算法的时间复杂度均为,排序效率较低,而对于排序,结合二分法和归并思想能够有效提升算法查询效率,本部分中介绍时间复杂度的排序算法。
归并排序
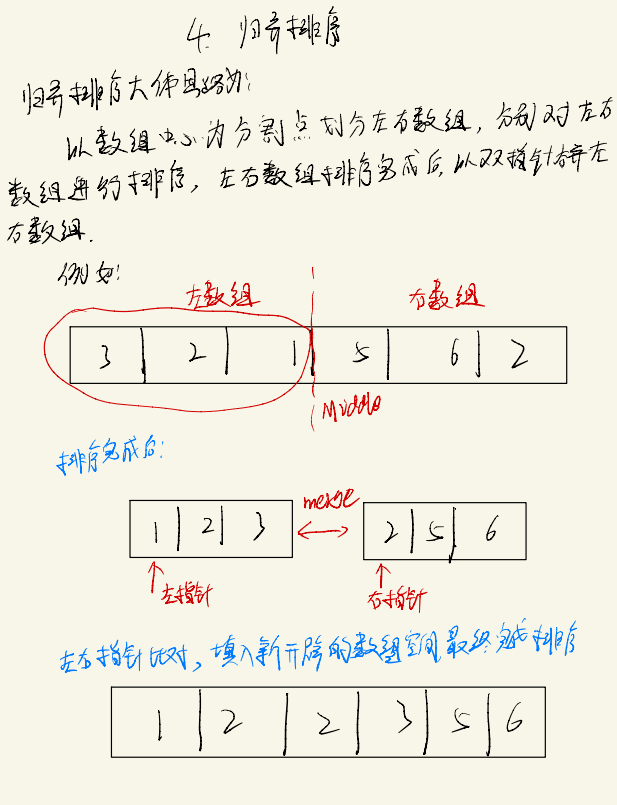
算法思路
归并排序通过递归地划分左右数组,对左右数组完成排序后,再合并两个数组,完成最终数组的排序,算法思路如下:
代码实现
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| package p2.sort_nlogn;
import java.util.Scanner;
public class MergeSort {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("请输入排序数字个数==========>");
int n = sc.nextInt();
int[] nums = new int[n];
System.out.println("请输入数据============>");
for (int i = 0; i < n; i++) {
nums[i]= sc.nextInt();
}
mergeSort(nums);
for (int num : nums) {
System.out.print(num + " ");
}
}
private static void mergeSort(int[] nums) {
if(nums == null || nums.length < 2){
return;
}
sort(nums, 0, nums.length - 1);
}
private static void sort(int[] nums, int l, int r) {
if(l == r){
return;
}
int m = l + (r - l) / 2;
sort(nums, l , m);
sort(nums, m+1, r);
merge(nums, l, m, r);
}
private static void merge(int[] nums, int l, int m, int r) {
int[] arr = new int[r - l + 1];
int index = 0;
int i = l;
int j = m + 1;
while(i <= m && j <= r){
arr[index++] = nums[i] <= nums[j] ? nums[i++]:nums[j++];
}
while(i <= m){
arr[index++] = nums[i++];
}
while(j <= r){
arr[index++] = nums[j++];
}
for (int k = 0; k < arr.length; k++) {
nums[l + k] = arr[k];
}
}
}
|
以master公式计算其时间复杂度为
其中a=2, b=2, d=1即
所以其时间复杂度为
归并排序时间复杂度低的原因是,相比于part1中提到的时间复杂度为的排序算法,
这些算法每一次排序过程都要经过一个长时间的元素比较,浪费了大量的比较次数。而归并排序中,每一次合并的两个数组都是有序的,这大大降低了比对次数,从而降低了算法的时间复杂度
由于归并排序中借用了其它数组完成数组的合并,因而该排序为外排序算法
额外空间复杂度为
思考:

快速排序
算法思路
快速排序经历了多个版本的迭代优化,不同版本基本思路如下:


代码实现
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| package p2.sort_nlogn;
import com.sun.org.apache.bcel.internal.generic.SWAP;
import jdk.internal.org.objectweb.asm.commons.StaticInitMerger;
import java.util.Scanner;
public class Code02_QuickSort {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("请输入排序数字个数==========>");
int n = sc.nextInt();
int[] nums = new int[n];
System.out.println("请输入数据============>");
for (int i = 0; i < n; i++) {
nums[i] = sc.nextInt();
}
quickSort(nums);
for (int num : nums) {
System.out.print(num + " ");
}
}
private static void quickSort(int[] nums) {
if(nums == null || nums.length < 2){
return;
}
sort(nums, 0, nums.length-1);
}
private static void sort(int[] nums, int l, int r) {
if(l < r){
swap(nums, r, l + (int)Math.random() * (r - l + 1));
int[] p = partition(nums, l, r);
sort(nums, l, p[0] - 1);
sort(nums, p[1] + 1, r);
}
}
private static int[] partition(int[] nums, int l, int r) {
int less = l - 1;
int more = r;
while(l < more){
if(nums[l] < nums[r]){
swap(nums, ++less, l++);
}else if(nums[l] > nums[r]){
swap(nums, --more, l);
}else{
l++;
}
}
swap(nums, more, r);
return new int[]{less + 1, more};
}
private static void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
|
时间复杂度上,快速排序对于有序的数组(例如[1,2,3,4,5,6,7,8,9]),其排序性能差,按照最坏情况下的复杂度算为
额外空间复杂度
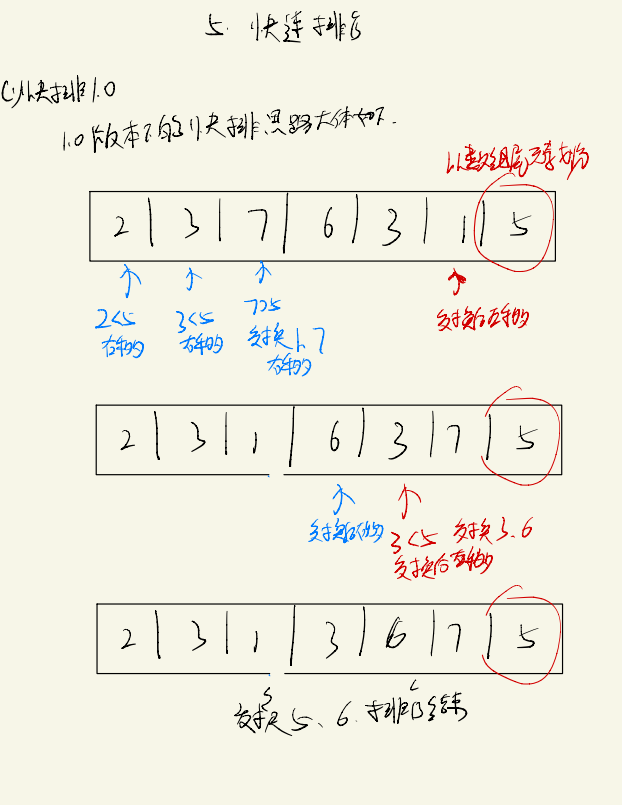
以一个实例加深对该快排思路的理解:

总结
本节中介绍了部分排序效率更高的算法,这些算法通过二分递归等思想降低了之前的一些简单排序算法中,存在的历史对比信息浪费,从而导致算法效率低的问题。







