Boom LeetCode入门（七）前缀树 & 贪心算法

发表于 更新于 分类于 阅读次数：

前缀树

基本思路

前缀树用于存储字符串等数据的结构，其插入和删除流程大体如↓：

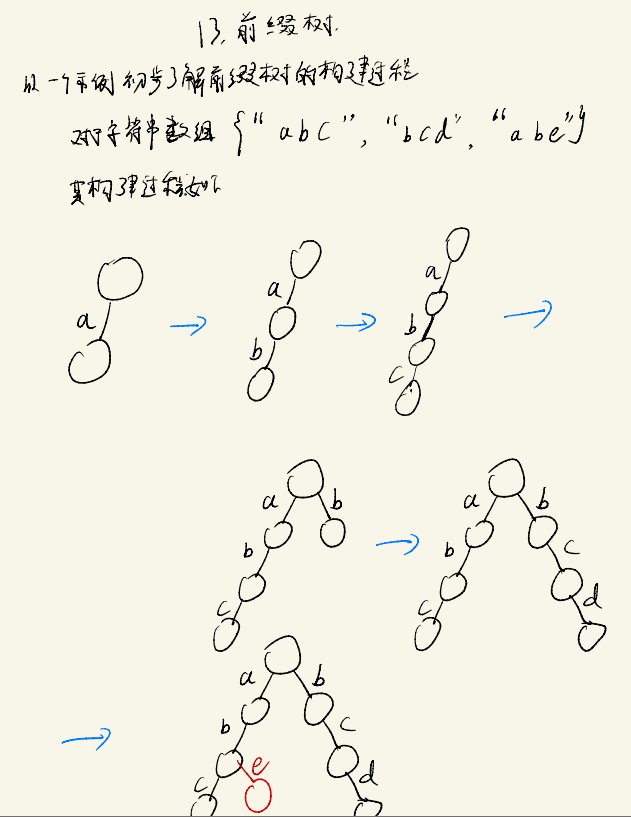
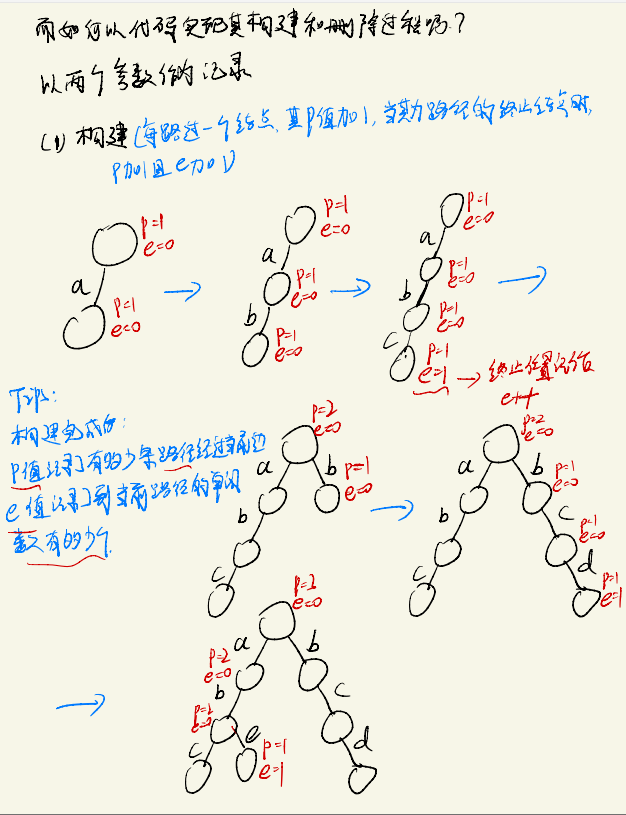
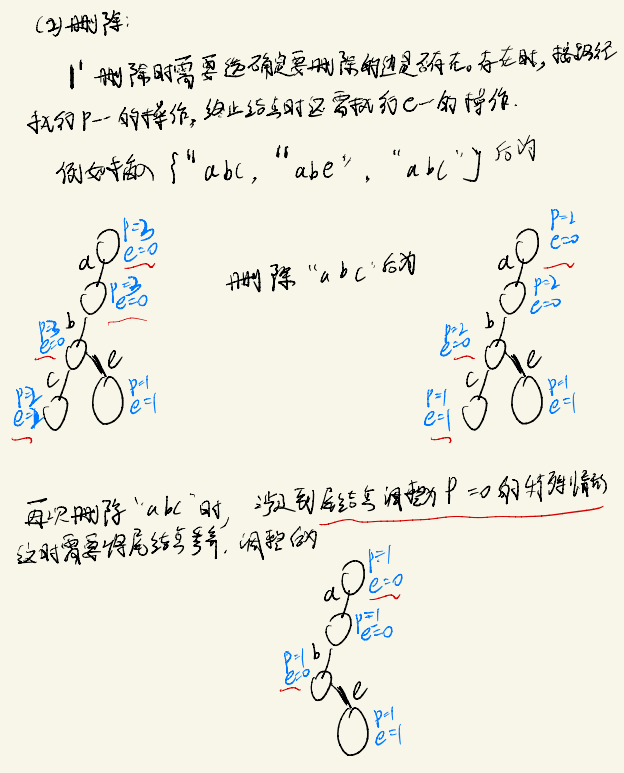
具体实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
package p7.preTreeAndGreedy;

/**
 * @PackageName:p7.preTreeAndGreedy
 * @ClassName:PreTree
 * @Description:前缀树
 * @author:sliu
 * @data 2022/5/21 19:51
 */
public class PreTree {
    public class preNode{
        //p值用于有多少个字符串路径经过当前路径
        int pass;
        //e值用于记录以当前节点为终止节点的路径有多少条
        int end;
        preNode[] nexts;

        public preNode(){
            pass = 0;
            end = 0;
            //nexts用于记录到0-26对应的字母a-z是否存在
            //nexts[0] == null表示没有走向a的路径
            //nexts[0] != null表示有走向a的路径，且存储了路径的下一个节点
            //next[25] == null表示没有走向z的路径
            nexts = new preNode[26];
        }
    }

    //初始化根节点
    preNode root = new preNode();

    //将所传入字符串插入前缀树中
    public void insert(String word){
        if(word == null){
            return;
        }
        char[] arr = word.toCharArray();
        preNode node = root;
        node.pass++;
        for (int i = 0; i < arr.length; i++) {

            int index = arr[i] - 'a';
            if(node.nexts[index] == null){
                node.nexts[index] = new preNode();
            }
            node = node.nexts[index];
            node.pass++;
        }
        //终止节点除p值增加外，e值也增加
        node.end++;
    }

    //查询字符串加入过几次
    public int search(String word){
        if(word == null){
            return 0;
        }
        preNode node = root;
        char[] arr = word.toCharArray();
        for (int i = 0; i < arr.length; i++) {
            int index = arr[i] - 'a';
            if(node.nexts[index] == null){
                return 0;
            }
            node = node.nexts[index];
        }
        //返回最终节点的e值即为字符串加入次数
        return node.end;
    }

    //有多少个单词是以当前所传入word为前缀的，例如以ab为前缀的是abc、abd等
    public int pathNumber(String word){
        if(word == null){
            return 0;
        }
        preNode node = root;
        char[] arr = word.toCharArray();
        for (int i = 0; i < arr.length; i++) {
            int index = arr[i] - 'a';
            if(node.nexts[index] == null){
                return 0;
            }
            node = node.nexts[index];
        }
        //返回最后一个字符的p值
        return node.pass;
    }

    //删除所传入字符串的路径
    public void delete(String word){
        //word不存在时，不进行删除操作
        if(word == null || search(word) == 0){
            return;
        }
        char[] arr = word.toCharArray();
        preNode node = root;
        for (int i = 0; i < arr.length; i++) {
            int index = arr[i] - 'a';
            if(--node.nexts[index].pass == 0){
                //当某个节点的p值为0时，应当直接对后续的全部路径进行剪枝操作
                node.nexts[index] = null;
                return;
            }
        }
        //终止节点的e值减1
        --node.end;
    }
}

贪心算法

经典贪心算法题解

会议室日程安排

题目：一个项目占用一个会议室，会议室同时只能被一个项目占用。给你每个项目的开始和结束时间，请给出最多能够完成多少场项目的宣讲，返回该场次数。

求解思路：

该问题的求解中贪心策略体现在，将尽可能早结束的会议安排进行程，就能得到最优解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
package p7.preTreeAndGreedy;

import java.util.Arrays;
import java.util.Comparator;

/**
 * @PackageName:p7.preTreeAndGreedy
 * @ClassName:Code02_Greedy_Room
 * @Description:贪心算法求解最大会议场次数
 * @author:sliu
 * @data 2022/5/21 20:42
 */
public class Code02_Greedy_Room {
    //存储会议时间戳
    class roomTime{
        //会议开始与结束时间
        int begin;
        int end;
        public roomTime(int begin, int end){
            this.begin = begin;
            this.end = end;
        }
    }

    public class myComparator implements Comparator<roomTime>{

        @Override
        public int compare(roomTime o1, roomTime o2) {
            return o1.end - o2.end;
        }
    }

    //返回从时间点timePot开始能够进行的最多场次会议
    public int maxNum(roomTime[] roomTimesSet, int timePot){
        if(roomTimesSet == null){
            return 0;
        }
        Arrays.sort(roomTimesSet, new myComparator());
        if(timePot < roomTimesSet[0].begin){
            return 0;
        }
        //记录能够开展的会议场次数
        int res = 0;
        for (int i = 0; i < roomTimesSet.length; i++) {
            if(timePot <= roomTimesSet[i].end){
                res++;
                timePot = roomTimesSet[i].end;
            }
        }
        return res;
    }
}

分金条

算法思路：哈夫曼树，依托小根堆数据结构，每次取出小根堆顶端的两个数，求其和，将和累加进最小代价，并将和放入小根堆，重复此操作，直到小根堆不足两个数时，返回最小代价。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
package p7.preTreeAndGreedy;

import java.util.PriorityQueue;

/**
 * @PackageName:p7.preTreeAndGreedy
 * @ClassName:Code03_Greedy_splitGold
 * @Description:贪心算法求解最小分黄金代价
 * @author:sliu
 * @data 2022/5/21 21:24
 */
public class Code03_Greedy_splitGold {
    public int splitGold(int[] arr){
        if(arr == null){
            return 0;
        }
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        for (int i = 0; i < arr.length; i++) {
            queue.add(arr[i]);
        }
        int res = 0;
        while(queue.size() > 1){
            int temp = queue.poll() + queue.poll();
            res += temp;
            queue.add(temp);
        }
        return res;
    }
}

求最大资金数

该题求解思路为，每次选择能够执行项目中，利润最大的项目。这样本金能够得到最大程度的上升。

借助两个堆来实现该方案，首先借助一个小根堆，小根堆中依据项目所需本金升序排列项目，每次根据所拥有的本金从小根堆中出队列。出队列的项目入另一个大顶堆，大顶堆依据项目的利润降序排列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
package p7.preTreeAndGreedy;

import java.util.Comparator;
import java.util.PriorityQueue;

/**
 * @PackageName:p7.preTreeAndGreedy
 * @ClassName:Code03_Greedy_MaxMoney
 * @Description:贪心算法求解最大收益
 * @author:sliu
 * @data 2022/5/21 21:39
 */
public class Code03_Greedy_MaxMoney {
    class project{
        //项目所需花费资金
        int cost;
        //项目所能获得的利润
        int profit;

        public project(int cost, int profit){
            this.cost = cost;
            this.profit = profit;
        }
    }

    //小根堆中依据花费升序排列
    public class costComparator implements Comparator<project>{

        @Override
        public int compare(project o1, project o2) {
            return o1.cost - o2.cost;
        }
    }

    //大根堆中依据利润降序排列
    public class profitComparator implements Comparator<project>{

        @Override
        public int compare(project o1, project o2) {
            return o2.profit - o1.profit;
        }
    }

    //num：允许做几次项目，money：初始资金
    public int maxMoney(project[] projects, int num, int money){
        if(projects == null){
            return 0;
        }
        PriorityQueue<project> minCostQueue = new PriorityQueue<>(new costComparator());
        for (project p : projects) {
            minCostQueue.add(p);
        }
        PriorityQueue<project> maxProfitQueue = new PriorityQueue<>(new profitComparator());
        int res = money;
        for (int i = 0; i < num; i++) {
            while(!minCostQueue.isEmpty() && minCostQueue.peek().cost <= monry){
                maxProfitQueue.add(minCostQueue.poll());
            }
           if(maxProfitQueue.isEmpty()){
               return res;
           }
           res += maxProfitQueue.poll().profit;
        }
        return res;
    }
}

拓展：如何通过1个大根堆+1个小根堆实现，实时返回一个数组的中位数？

规则如下：

  • 第一个数直接入大根堆
  • 后续进入的数，如果大于大根堆堆顶的数，入大根堆，否则入小根堆
  • 如果大小堆size大小相差2，将size较大的堆堆顶元素出队，并入队另一个堆

这样，当大小堆size相等时，去两个堆堆顶元素的平均数，不想等时，取size较大那一个堆的堆顶元素，就能取得当前数组中位数。

总结

本节讲解了如何构建一颗前缀树，并实现对树的编辑。学习了贪心算法，需要注意的是贪心算法并没有固定的解题模板，其思路依据场景的变化而变化，需要多尝试，利用对比器进行检验，验证其有效性。